La conception

Vous ne le savez peut-être pas, mais Michael Rao, un mathématicien français de 37 ans du CNRS et de l’École Normale Supérieure de Lyon, dans sa thèse a fait une démonstration qui a mis fin à la classification des polygones convexes, en incluant les pentagones. Plus précisément les pentagones irréguliers, qui couvrent le plan euclidien sans laisser un trou, et rend ainsi le pavage possible contrairement aux pentagones réguliers. Ces structures étonnantes et magnifiques, défient pourtant les mathématiciens, qui peinent à en donner la définition. Cela confère à ces formes une asymétrie captivante et une variété visuelle qui peut être utilisée de manière créative dans des conceptions artistiques et architecturales.

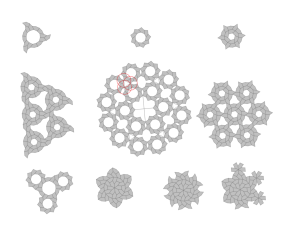
Dans le contexte d’un plafond artistique, l’utilisation de pentagones irréguliers pourrait créer un motif intégrant et unique. La diversité des formes des pentagones ajoute une complexité visuelle, tandis que leurs différences de tailles selon leur positionnement offrent un dynamisme esthétique. Lorsqu’ils sont disposés de manière réfléchie, ces pentagones peuvent contribuer à la création d’un motif visuellement stimulant, évoquant une sensation de modernité d’originalité.

Ainsi, le pentagone irrégulier d’angles distinctes mais aux côtés égaux étaient retenu pour créer le motif choisi. Cependant, il ne générait pas un maillage linéaire que celui formé par le pentagone irrégulier isocèle permettant ainsi de mieux gérer l’emplacement dans une pièce à angle droit par exemple.

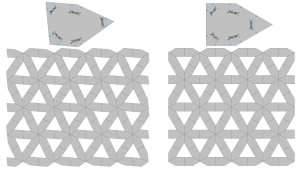
La modélisation

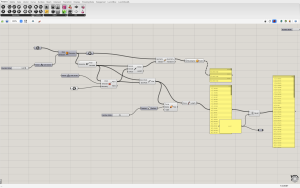
Ce motif ainsi retenu, est transféré sur rhino. Il sert alors de base (point de départ) pour la conception et la modélisation par GrassHopper. Ces pentagones transformés en poly-surfaces sont groupés en une fonction appelée Surface. Celle-ci est ensuite transformée en volume par la fonction Extrude, guidé par un Slider permettant de varier l’épaisseur des pentagones. Cette dernière est par la suite, rendu solide par la fonction m² area. Puis, elle est projetée par la fonction Project point sur une Surface à double courbure. La fonctionLine, ici permet de donner cet effet suspendu (à des câbles ou un cylindré métallique) en reliant les point de bases aux points projetés, suivie de la fonction Pipe qui permet de jouer sur l’épaisseur des câbles ou cylindrés.

La fonction Lenght, suivie de celle dite Panel nous permettent, en fin de compte, de connaître la longueur selon l’échelle, de ces différents câbles. La touche finale consiste à rendre le modèle visible sur Rhino par la fonction Bake.

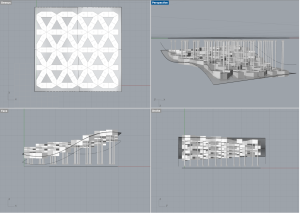
En projetant ces pentagones irréguliers sur une surface à double courbure, l’effet est amplifié, car la courbure crée des jeux de lumière et d’ombre, ajoutant une dimension supplémentaire à l’expérience visuelle. La variation des niveaux des pentagones, induite par la double courbure de la surface, intensifie cette dynamique, offrant une perspective changeante selon le point de vue de l’observateur.

La maquette

La création d’une maquette imprimée en 3D aurait pu être une option intéressante, mais elle présentait le risque de compromettre rapidement l’aspect caractéristique des modules pentagonaux irréguliers. Cet aspect est crucial, car il crée l’illusion visuelle qu’ils orbitent les uns autour des autres, évoquant ainsi une sensation d’apesanteur. Pour préserver cette caractéristique, j’ai pris la décision d’opter plutôt pour une méthode de découpe laser des modules, réalisée sur du carton d’une épaisseur de 2 mm.

En choisissant la découpe laser, nous pouvons mieux contrôler les contours et les détails des modules, préservant ainsi leur forme pentagonale irrégulière. Cette approche offre également la possibilité de jouer sur l’épaisseur des modules en superposant différentes couches de carton. Cette stratégie de superposition permet non seulement de reproduire fidèlement l’apparence des modules en orbite, mais elle offre également une flexibilité dans la création de variations d’épaisseur, renforçant ainsi l’effet visuel recherché. En résumé, la découpe laser sur carton offre une solution plus précise pour reproduire l’esthétique désirée tout en préservant l’élément unique des modules en orbite.

En utilisant les hauteurs des suspentes obtenues grâce à la fonction Panel, j’ai la capacité de découper les baguettes de bois à l’échelle précise de la maquette. En intégrant au bout de ces baguettes les modules que j’ai fabriqués, je parviens ainsi à reproduire fidèlement la géométrie et la disposition des éléments à l’échelle réduite.

L’aspect particulièrement intéressant de cette approche réside dans l’utilisation du codage sur Grasshopper. Grâce à cette plateforme, une simple fonction génère l’ensemble des paramètres nécessaires à la conception de la maquette ou de l’objet à l’échelle voulue. Cela simplifie considérablement le processus de conception en automatisant la génération des éléments, assurant ainsi une cohérence et une précision remarquables dans l’échelle souhaitée.

L’utilisation de Grasshopper offre une flexibilité significative en permettant des ajustements rapides et efficaces. Cela s’avère particulièrement avantageux pour expérimenter avec différentes configurations et dimensions, tout en assurant une cohérence globale dans le résultat final. En résumé, le codage sur Grasshopper optimise le processus de conception en fournissant une approche efficace et précise pour créer une maquette ou un objet à l’échelle avec une grande facilité d’ajustement.

Le projet

En résumé, l’utilisation de pentagones irréguliers dans la conception d’un plafond apporte une touche artistique distinctive, captivante et innovante, transformant l’espace en un environnement visuellement stimulant et harmonieux. De plus le choix du bois comme matériau pour le plafond cinétique apporte plusieurs avantages et caractéristiques uniques, contribuant à créer une atmosphère chaleureuse, esthétique et fonctionnelle : esthétique chaleureuse, flexibilité de conception, légèreté, durabilité, adaptabilité aux mouvements et écologie.

La suite sera d’intégrer ce plafond dans un projet (je vous en ferais part en février)

Jacques Andhy Leger,

Etudiant en master 2

20506

Paris La Villette.